The problematic effect of small effects

Why do ecologists often get different answers to the same question? Depending on the study, for example, the relationship between biodiversity and ecosystem function could be positive, negative, or absent (e.g. Cardinale et al. 2012). Ecologists explain this in many ways - experimental issues and differences, context dependence. However, it may also be due to an even simpler issue, that of the statistical implications of small effect sizes.

This is the point that Lemoine et al. make in an interesting new report in Ecology. Experimental data from natural systems (e.g. for warming experiments, BEF experiments) is often highly variable, has low replication, and effect sizes are frequently small. Perhaps it is not surprising we see contradictory outcomes, because data with small true effect sizes are prone to high Type S (reflect the chance of obtaining the wrong sign for an effect) and Type M (the amount by with an effect size must be overestimated in order to be significant). Contradictory results arise from these statistical issues, combined with the idea that papers that do get published early on may simply have found significant effects by chance (the Winner's Curse). 

Power reflects the chance of failing to correctly reject the null hypothesis (Ho). The power of ecological experiments increases with sample size (N), since uncertainty in data decreases with increasing N. However, if your true effect size is small, studies with low power have to significantly overestimate the effect size to have a significant p-value. This is the result of the fact that if the variation in your data is large and your effect size is small, the critical value for a significant z-score is quite large. Thus for your results to be significant, you need to observe an effect larger than this critical value, which will be much larger than the true effect size. It's a catch-22 for small effect sizes: if your result is correct, it very well may not be significant; if you have a significant result, you may be overestimating the effect size. 

From Lemoine et al. 2016. 

The solution to this issue is clearly a difficult one, but the authors make some useful suggestions. First, it's really the variability of your data, more than the sample size, that raises the Type M error. So if your data is small but beautifully behaved, this may not be a huge issue for you (but you must be working in a highly atypical system). If you can increase your replication, this is the obvious solution. But the other solutions they see are cultural shifts when we publish statistical results. As with many other, the authors suggest we move away from reliance on p-values as a pass/fail tool for results. In addition to reporting p-values, they suggest we report effect sizes and their error rates. Further, that this be done for all variables regardless of whether the results are significant. Type M error and power analyses can be reported in a fashion meant to inform interpretation of results: “However, low power (0.10) and high Type M error (2.0) suggest that this effect size is likely an overestimate. Attempts to replicate these findings will likely fail.” 

Lemoine, N. P., Hoffman, A., Felton, A. J., Baur, L., Chaves, F., Gray, J., Yu, Q. and Smith, M. D. (2016), Underappreciated problems of low replication in ecological field studies. Ecology. doi: 10.1002/ecy.1506

#ESA100 : Statistical Steps to Ecological Leaps

By Marc Cadotte and Caroline Tucker

For their centennial, ESA is asking their members identify as the ecological milestones of the last 100 years. They’ve asked the EEB & Flow to consider this question as a blog post. And there are many – ecology has grown from an amateur mix of natural history and physiology to a relevant and mature discipline. Part of this growth rests on major theoretical developments from great ecologists like Clements, Gleason, MacArthur, Whittaker, Wilson, Levins, Tilman and Hubbell. These people provided the ideas needed to move ecology to new territory. But ideas on their own aren’t enough, in the absence of necessary tools and methods. Instead, we argue that modern ecology would not exist without statistics.

The most cited paper in ecology and evolutionary biology is a methodological one (Felsenstein’s 1985 paper on phylogenetic confidence limits in Evolution – cited over 26,000 times) (Felsenstein, 1985). Statistics is the backbone that ecology develops around. Every new statistical method potentially opens the door to new ways of analyzing data and perhaps new hypotheses. To this end, we show how seven statistical methods changed ecology.

1. P-values and Hypothesis Testing – Setting standards for evidence.

Ecological papers in the early 1900s tended to be data-focused. And that data was analyzed in statistically rudimentary ways. Data was displayed graphically, perhaps with a simple model (e.g. regression) overlaid on the plot. Scientists sometimes argued that statistical tests offered no more than confirmation of the obvious.

At the same time, statistics were undergoing a revolution focused on hypothesis testing. Karl Pearson started it, but Ronald Fisher (Fisher 1925) and Pearson’s son Egon and Jerzy Neyman (Neyman & Pearson 1933) produced the theories that would change ecology. These men gave us the p-value – ‘the probability to obtain an effect equal to or more extreme than the one observed presuming the null hypothesis of no effect is true’ and gave us a modern view of hypothesis testing – i.e. that a scientist should attempt to reject a null hypothesis in favour of some alternative hypothesis.

It’s amazing to think that these concepts are now rote memorization for first year students, having become so ingrained into modern science. Hypothesis testing using some pre-specified level of significance is now the default method for looking for evidence. The questions asked, choices about sample size, experimental design and the evidence necessary to answer questions were all framed in the shadow of these new methods. p-values are no longer the only approach to hypothesis testing, but it is incontestable that Pearson and Fisher laid the foundations for modern ecology. (See Biau et al 2010 for a nice introduction).

2. Multivariate statistics: Beginning to capture ecological complexity.

Because the first emergence of statistical tests arose from agricultural studies, they were designed to test for differences from among treatments or from known distributions. They applied powerfully to experiments manipulating relatively few factors and measuring relatively few variables. However, these types of analyses did not easily permit investigations of complex patterns and mechanisms observed in natural communities.

Often what community ecologists have in hand are multiple datasets about communities including species composition and abundance, environmental measurements (e.g. soil nutrients, water chemistry, elevation, light, temperature, etc.), and perhaps distances between communities. And what researchers want to know is how compositional (multi-species) change among communities is determined by environmental variables. We shouldn’t understate the importance of this type of analysis on communities, in one tradition of community ecology, we would simply analyze changes in richness or diversity. But communities can show a lack of variation in diversity even when communities are being actively structured: diversity is simply the wrong currency.

Many of the first forays into multivariate statistics were through measuring the compositional dissimilarity or distances between communities. For example Jaccard (Jaccard, 1901), and Bray and Curtis (Bray & Curtis, 1957) are early ecologists that invented distance-based measures. Correlating compositional dissimilarity with environmental differences required ordination techniques. Principle Component Analysis (PCA) was actually invented by Karl Pearson around 1900 but computational limitations constrained its use until the 1980s. Around this time, other methods began to emerge which ecologists started to employ (Hill, 1979; Mantel, 1967). The development of new methods continues today (e.g. Peres-Neto & Jackson, 2001), and the use of multivariate analysis is a community ecology staple.

There are now full texts dedicated to the implementation of multivariate statistical tests with ecological data (e.g., Legendre & Legendre, 1998). Further, there are excellent resources available in R (more on this later) and especially in the package vegan (Oksanen et al., 2008), which implements most major multivariate methods. Going forward it is clear that multivariate techniques will continue to be reassessed and improved (e.g. Guillot & Rousset, 2013), and there will be a greater emphasis on the need to articulate multivariate hypotheses and perhaps use multivariate techniques to predict communities (Laughlin, 2014) –not just explain variation.

3. Null models: Disentangling patterns and processes.

Ecology occurs over large spatial and temporal scales, and so it is always reliant on observational data. Gathering observational data is often much easier than doing experimental work at the same spatial or temporal scale, but it is also complicated to analyze. Variation from a huge number of unmeasured variables could well weaken patterns or create unexpected ones. Still, the search for patterns drove the analysis of observational data: including patterns along environmental gradients, patterns in species co-occurrences, patterns in traits. The question of what represented a meaningful pattern was harder to answer.

It seems that ecology could not go on looking at patterns forever. But it took some heated arguments finally change this. The ‘null model wars’ revolved around Jared Diamond’s putative assembly rules for birds on islands (Diamond 1975), which relied on a “checkerboard” pattern of species co-occurrences. The argument for null models was led by Connor and Simberloff (Connor & Simberloff 1979) and later joined by Nicholas Gotelli (e.g. Gotelli & Graves 1996). A null model, they point out, was necessary to determine whether observed patterns of bird distribution were actually different from random patterns of apparent non-independence between species pairs. Further, other ecological mechanisms (different habitat requirements, speciation, dispersal limitations) could also produce non-independence between species pairs. The arguments about how to appropriately formulate null models have never completely ended (e.g., 1, 2, 3), but they now drive ecological analyses. Tests of species-area relationships, phylogenetic diversity within communities, limiting similarity of body sizes or traits, global patterns of diversity, species co-occurrences, niche overlaps, and nestedness in networks, likely all include a null model of some sort.

The null model wars have been referred to as a difficult and contentious time for ecology. Published work (representing significant amounts of time and funding) perhaps needed to be re-evaluated to differentiate between true and null ecological patterns. But despite these growing pains, null models have forced ecology to mature beyond pattern-based analyses to more mechanistic ones.

4. Spatial statistics: Adding distance and connectivity.

Spatially-explicit statistics and models seem like an obvious necessity for ecology. After all, the movement of species through space is an immensely important part of their life history, and further, most ecologically relevant characteristics of the landscapes vary through space, e.g. resources, climate, and habitat. Despite this, until quite recently ecological models tended to assume a uniform distribution of species and processes through space, and that species’ movement was uniform or random through space. The truism that points close in space, all else being equal, should be more similar than distant points, while obvious, also involved a degree of statistical complexity and computing requirements difficult to achieve.

Fortunately for ecology, the late 1980s and early 1990s were a time of rapid computing developments that enabled the incorporation of increasing spatial complexity into ecological models (Fortin & Dale 2005). Existing methods – some ecological, some borrowed from geography – were finally possible with available technology, including nearest neighbour distances, Ripley’s K, variograms, and the Mantel test (Fortin, Dale & ver Hoef 2002). Ideas now fundamental to ecology such as connectivity, edge effects, spatial scale (“local” vs. “regional”), spatial autocorrelation, and spatial pattern (non-random, non-uniform spatial distributions) are the inheritence of this development. Many fields of ecology have incorporated spatial methods or even owe their development to spatial ecology, including meta-communities, landscape ecology, conservation and management, invasive species, disease ecology, population ecology, and population genetics. Pierre Legendre asked in his seminal paper (Legendre 1993) on the topic whether space was trouble, or a new paradigm. It is clear that space was an important addition to ecological analyses.

5. Measuring diversity: rarefaction and diversity estimators.

How many species are there in a community? This is a question that inspires many biologists, and is something that is actually very difficult to measure. Cryptic, dormant, rare and microscopic organisms are often undersampled, and accurate estimates of community diversity need to deal with these undersampled species.

Communities may seem to have different numbers of species simply based on the fact some have been sampled more thoroughly. Unequal sampling effort can distort real differences or similarities in the numbers of species. For example, in some recent analyses of plant diversity using the freely available species occurrence data from GBIF, we found that Missouri seems to have the highest plant diversity –a likely outcome of the fact that the Missouri Botanical Gardens routinely samples local vegetation and makes the data available. Estimating diversity from equalized sampling effort was developed by a number of ecologists (Howard Sanders, Stuart Hurlbert, Dan Simberloff, and Ken Heck) in the 1960s and 1970s resulting in modern rarefaction techniques.

Sampling effort was one problem, and ecologists also recognized that even with equivalent sampling effort, we are likely missing rare and cryptic species. Most notably Anne Chao and Ramon Margalef developed a series of diversity estimators in the 1980s-1990s. These types of estimators place emphasis on the numbers of rare species, because these give insight into the unobserved species. All things being equal, the community with more rare species likely has more unobserved species. These types of estimators are particularly important when we need to estimate the ‘true’ diversity form a limited number of samples. For example, researchers at Sun Yat-sen University in Guangzhou, China, recently performed metagenomic sampling of almost 2000 soil samples from a 500x1500 m forest plot. From these samples they used all known diversity estimators and have come to the conclusion that there are about 40,000 species of bacteria and 16,000 species of fungi in this forest plot! This level of diversity is truly astounding, and without genetic sampling and the suite of diversity estimators, we would have no way of knowing that there is this amazing, complex world beneath our feet.

As we move forward, researchers are measuring diversity in new ways, by quantifying phylogenetic and functional diversity and we will need new methods to estimate these for entire communities and habitats. Anne Chao, and colleagues have recently published a method to estimate true phylogenetic diversity (Chao et al., 2014).

6. Hierarchical and Bayesian modelling: Understanding complex living systems.

Each previous section reinforces the fact that ecology has embraced statistical methods that allow it to incorporate complexity. Accurately fitting models to observational data might require large numbers of parameters with different distributions and complicated interconnections. Hierarchical models offer a bridge between theoretical models and observational data: they can account for missing or biased data, latent (unmeasured) variables, and model uncertainty. In short, they are ideal for the probabilistic nature of ecological questions and predictions (Royle and Dorazio, 2008). The computational and conceptual tools have greatly advanced over the past decade, with a number of good computer programs (e.g., BUGS ) available and several useful texts (e.g., Bolker 2008).

The usage of these types of models has been closely (but not exclusively) tied to Bayesian approaches to statistics. Bayesian statistics have had much written about them, and not a little controversy beyond the scope of this post (but see these blogs for lots of interesting discussion). The focus is on assigning a probability distribution to a hypothesis (the prior distribution) which can be updated sequentially as more information is obtained. Such an approach may have natural similarities to management and applied practices in ecology, where expert or existing knowledge is already incorporated into decision making and predictions informally. Often though, hierarchical models can be tailored to better fit our hypotheses than traditional univariate statistics. For example, species occupancy or abundance can be modelled as probabilities based on detection error, environmental fit and dispersal likelihood.

There is so much that can be said about hierarchical and bayesian statistical models, and their incorporation into ecology is still in progress. The promise from these methods that the complexity inherent in ecological processes can be more closely captured by statistical models and that model predictions are improving, is one of the most important developments in recent years. 

7. The availability, community development and open sharing of statistical methods.

The availability of and access to statistical methods today is unparalleled in any time in human history. And it is because of the program R. There was a time recently where a researcher might have had to purchase a new piece of software to perform a specific analysis, or that they would have to wait years for new analyses to become available. The rise of this availability of statistical methods is threefold. First, R is freely available without any fees limiting access. Second, is that the community of users contribute to it, meaning that specific analyses required for different questions are available, and often formulated to handle the most common types of data. Finally, new methods appear in R as they are developed. Cutting edge techniques are immediately available, further fostering their use and scientific advancement.

References

Bolker, B. M. (2008). Ecological models and data in R. Princeton University Press.

Bray, J. R., & Curtis, J. T. (1957). An Ordination of the Upland Forest Communities of Southern Wisconsin. Ecological Monographs, 27(4), 325–349. doi:10.2307/1942268

Chao, A., Chiu, C.-H., Hsieh, T. C., Davis, T., Nipperess, D. A., & Faith, D. P. (2014). Rarefaction and extrapolation of phylogenetic diversity. Methods in Ecology and Evolution, n/a–n/a. doi:10.1111/2041-210X.12247

Connor, E.F. & Simberloff, D. (1979) The assembly of species community: chance or competition? Ecology, 60, 1132-1140.

Diamond, J.M. (1975) Assembly of species communities. Ecology and evolution of communities (eds M.L. Cody & J.M. Diamond), pp. 324-444. Harvard University Press, Massachusetts.
Felsenstein, J. (1985). Confidence limits on phylogenies : An approach using the bootstrap. Evolution, 39, 783–791.

Fisher, R.A. (1925) Statistical methods for research workers. Oliver and Boyd, Edinburgh.
Fortin, M.-J. & Dale, M. (2005) Spatial Analysis: A guide for ecologists. Cambridge University Press, Cambridge.

Fortin, M.-J., Dale, M. & ver Hoef, J. (2002) Spatial analysis in ecology. Encyclopedia of Environmetrics (eds A.H. El-Shaawari & W.W. Piegorsch). John Wiley & Sons.
Gotelli, N.J. & Graves, G.R. (1996) Null models in ecology. Smithsonian Institution Press Washington, DC.

Guillot, G., & Rousset, F. (2013). Dismantling the Mantel tests. Methods in Ecology and Evolution, 4(4), 336–344. doi:10.1111/2041-210x.12018
Hill, M. O. (1979). DECORANA — A FORTRAN program for Detrended Correspondence Analysis and Reciprocal Averaging.

Jaccard, P. (1901). Etude comparative de la distribution florale dans une portion des Alpes et du Jura. Bulletin de La Societe Vaudoise Des Sciences Naturelle, 37, 547–579.

Laughlin, D. C. (2014). Applying trait-based models to achieve functional targets for theory-driven ecological restoration. Ecology Letters, 17(7), 771–784. doi:10.1111/ele.12288

Legendre, P. (1993) Spatial autocorrelation: trouble or new paradigm? Ecology, 74.

Legendre, P., & Legendre, L. (1998). Numerical Ecology. Amsterdam: Elsevier Science B. V.

Mantel, N. (1967). The detection of disease clustering and a generalized regression approach. Cancer Research, 27, 209–220.

Neyman, J. & Pearson, E.S. (1933) On the problem of the most efficient tests of statistical hypotheses. PHilosophical Transactions of the Royal Society A, CCXXXL.

Oksanen, J., Kindt, R., Legendre, P., O’Hara, R., Simpson, G. L., Stevens, M. H. H., & Wagner, H. (2008). Vegan: Community Ecology Package. Retrieved from http://vegan.r-forge.r-project.org/

Peres-Neto, P. R., & Jackson, D. A. (2001). How well do multivariate data sets match? The advantages of a Procrustean superimposition approach over the Mantel test. Oecologia, 129, 169–178.

Royle and Dorazio. (2008). Hierarchical Modeling and Inference in Ecology. 

Links: Reanalyzing R-squares, NSF pre-proposals, and the difficulties of academia for parents

First, Will Pearse has done a great job of looking at the data behind the recent paper looking at declining R and p-values in ecology, and his reanalysis suggests that there is a much weaker relationship between r2 values and time (only 4% rather than 62% as reported). Because the variance is both very large within-years and also not equal through time, a linear model may not be ideal for capturing this relationship.
Thanks @prairiestopatchreefs for linking this.

From the Sociobiology blog, something that most US ecologists would probably agree on: the NSF pre-proposal program has been around long enough (~3 years) to judge on its merits, and it has not been an improvement. In short, pre-proposals are supposed to use a 5 page proposal to allow NSF to identify the best ideas and then invite those researchers to submit a full proposal similar to the traditional application. Joan Strassman argues that not only is this program more work for applicants (you must write two very different proposals in short order if you are lucky to advance), it offers very few benefits for them.

The reasons for the gender gap in STEM academic careers gets a lot of attention, and rightly so given the continuing underrepresentation of women. The demands of parenthood often receive some of the blame. The Washington Post is reporting on a study that considers parenthood from the perspective of male academics. The study took an interview-based, sociological approach, and found that the "majority of tenured full professors [interviewed] ... have either a full-time spouse at home who handles all caregiving and home duties, or a spouse with a part-time or secondary career who takes primary responsibility for the home." But the majority of these men also said they wanted to be more involved at home. As one author said, “Academic science doesn’t just have a gender problem, but a family problem...men or women, if they want to have families, are likely to face significant challenges.”

On a lighter note, if you've ever joked about PNAS' name, a "satirical journal" has taken that joke and run with it. PNIS (Proceedings of the Natural Institute of Science) looks like the work of bored post-docs, which isn't necessarily a bad thing. The journal has immediately split into two subjournals: PNIS-HARD (Honest and Real Data) and PNIS-SOFD (Satirical or Fake Data), which have rather interesting readership projections:

Debating the p-value in Ecology

It is interesting that p-values still garner so much ink: it says something about how engrained and yet embattled they are. This month’s Ecology issue explores the p-value problem with a forum of 10 new short papers* on the strengths and weaknesses, defenses and critiques, and various alternatives to “the probability (p) of obtaining a statistic at least as extreme as the observed statistic, given that the null hypothesis is true”.

The defense for p-values is lead by Paul Murtaugh, who provides the opening and closing arguments. Murtaugh, who has written a number of good papers about ecological data analysis and statistics, takes a pragmatic approach to null hypothesis testing and p-values. He argues p-values are not flawed so much as they are regularly and egregiously misused and misinterpreted. In particular, he demonstrates mathematically that alternative approaches to the p-value, particularly the use of confidence intervals or information theoretic criteria (e.g. AIC), simply present the same information as p-values in slightly different fashions. This is a point that the contribution by Perry de Valpine supports, noting that all of these approaches are simply different ways of displaying likelihood ratios and the argument that one is inherently superior ignores their close relationship. In addition, although acknowledging that cutoff values for significant p-values are logically problematic (why is a p-value of 0.049 so much more important than one of 0.051?), Murtaugh notes that cutoffs reflect decisions about acceptable error rates and so are not inherently meaningless. Further, he argues that dAIC cutoffs for model selection are no less arbitrary. 

The remainder of the forum is a back and forth argument about Murtaugh’s particular points and about the merits of the other authors’ chosen methods (Bayesian, information theoretic and other approaches are represented). It’s quite entertaining, and this forum is really a great idea that I hope will feature in future issues. Some of the arguments are philosophical – are p-values really “evidence” and is it possible to “accept” or “reject” a hypothesis using their values? Murtaugh does downplay the well-known problem that p-values summarize the strength of evidence against the null hypothesis, and do not assess the strength of evidence supporting a hypothesis or model. This can make them prone to misinterpretation (most students in intro stats want to say “the p-value supports the alternate hypothesis”) or else interpretation in stilted statements.

Not surprisingly, Murtaugh receives the most flak for defending p-values from researchers working in alternate worldviews like Bayesian and information-theoretic approaches. (His interactions with K. Burnham and D. Anderson (AIC) seem downright testy. Burnham and Anderson in fact start their paper “We were surprised to see a paper defending P values and significance testing at this time in history”...) But having this diversity of authors plays a useful role, in that it highlights that each approach has it's own merits and best applications. Null hypothesis testing with p-values may be most appropriate for testing the effects of treatments on randomized experiments, while AIC values are useful when we are comparing multi-parameter, non-nested models. Bayesian similarly may be more useful to apply to some approaches than others. This focus on the “one true path” to statistics may be behind some of the current problems with p-values: they were used as a standard to help make ecology more rigorous, but the focus on p-values came at the expense of reporting effect sizes, making predictions, or careful experimental design.

Even at this point in history, it seems like there is still lots to say about p-values.

*But not open-access, which is really too bad. 

P-values, the statistic that we love to hate

P-values are an integral part of most scientific analyses, papers, and journals, and yet they come with a hefty list of concerns and criticisms from frequentists and Bayesians alike. An editorial in Nature (by Regina Nuzzo) last week provides a good reminder of some of the more concerning issues with the p-value. In particular, she explores how the obsession with "significance" creates issues with reproducibility and significant but biologically meaningless results.

Ronald Fischer, inventor of the p-value, never intended it to be used as a definitive test of “importance” (however you interpret that word). Instead, it was an informal barometer of whether a test hypothesis was worthy of continued interest and testing. Today though, p-values are often used as the final word on whether a relationship is meaningful or important, on whether the the test or experimental hypothesis has any merit, even on whether the data is publishable. For example in ecology, significance values from a regression or species distribution model are often presented as the results. 

This small but troubling shift away from the original purpose for p-values is tied to concerns about false alarms and with replicability of results. One recent suggestion for increasing replicability is to make p-values more stringent - to require that they be less that 0.005. But the point the author makes is that although p-values are typically interpreted as “the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true”, this doesn't actually mean that a p-value of 0.01 in one study is exactly consistent with a p-value of 0.01 found in another study. P-values are not consistent or comparable across studies because the likelihood that there was a real (experimental) effect to start with alters the likelihood that a low p-value is just a false alarm (figure). The more unlikely the test hypothesis, the more likely a p-value of 0.05 is a false alarm. Data mining in particular will be (unwittingly) sensitive to this kind of problem. Of course one is unlikely to know what the odds of the test hypothesis are, especially a priori, making it even more difficult to correctly think about and use p-values. 

from: http://www.nature.com/news/scientific-method-statistical-errors-1.14700#/b5

The other oft-repeated criticism of p-values is that a highly significant p-value make still be associated with a tiny (and thus possibly meaningless) effect size. The obsession with p-values is particularly strange then, given that the question "how large is the effect?", should be more important than just answering “is it significant?". Ignoring effect sizes leads to a trend of studies showing highly significant results, with arguably meaningless effect sizes. This creates the odd situation that publishing well requires high profile, novel, and strong results – but one of the major tools for identifying these results is flawed. The editorial lists a few suggestions for moving away from the p-value – including to have journals require effect sizes and confidence intervals be included in published papers, to require statements to the effect of “We report how we determined our sample size, all data exclusions (if any), all manipulations and all measures in the study”, in order to limit data-mining, or of course to move to a Bayesian framework, where p-values are near heresy. The best advice though, is quoted from statistician Steven Goodman: “The numbers are where the scientific discussion should start, not end.”

How is a species like a baseball player?

Biomass is to runs as species is to player, and as ecologist is to Brad Pitt.

Community ecology and major league baseball have a lot to learn from each other.

Let's back up. As a community ecologist, I think about how species assemble into communities, and the consequences for ecosystems when species disappear. I'm especially interested using traits of species to address these issues. For the grassland plants that I often work with, the traits are morphological (for example, plant height and leaf thickness), physiological (leaf nitrogen concentration, photosynthetic rate), and life history (timing and mode of reproduction).

As a baseball fan, I spend a lot of time watching baseball. Actually, I'm watching my Red Sox now (multitasking as usual; I freely admit there's a lot of down time in between pitches). I care about how the team does, mostly in terms of beating the Yankees. I'm especially interested in how individual players are doing at any time; for fielders I care about their batting average and defensive skills, and for the pitchers I care about how few runs they allow and how many strikeouts they get.

So my vocation and avocation have some similarities. Both ecology and baseball have changed in the last decade or so to become more focused on 'granular' data at the individual level. In ecology this has been touted as a revolutionary shift in perspective, but is really a return to the important aspects of what roles organisms play in ecosystems, and how ecosystems are shaped by the organisms in them. This trait-based approach has shifted the collection and sharing of data on organism morphology, physiology, and life history into warp speed, to the great benefit of quantitatively-minded ecologists everywhere.

In baseball, the ability to collate and analyze data on every pitch and every play has lead to an explosion of new metrics to evaluate players. One of the simplest of these new metrics, which even the traditionalists in baseball now value, is "on base plus slugging" (OPS, see all the details here). This data-intensive approach to analyzing player performance was most famously championed by the manager of the Oakland Athletics in the late 1990's, now being played by Brad Pitt in the upcoming movie Moneyball.

There is no one ecologist in particular who can claim credit for popularizing trait-based approaches in community ecology, but for the sake of laughs let's make Owen Petchey the Brad Pitt analogue.

What can we do with this analogy? For pure nerd fun, we can think about what these two worlds can learn from each other.

What can baseball learn from community ecology?

One of the most notable trait-centric innovations in community ecology has been the use of functional diversity (FD), which represents how varied the species in a community are in terms of their functional traits. Many flavors of FD exist (one of which was authored by Owen Petchey, above), but the goal is to use one value to summarize the variation in functional traits of species in a community. A high value for a set of communities indicates greater distinctiveness among the community members, and is taken to represent greater niche complementarity.

For fun, I've taken stats from a fantastic baseball database[i] and calculated the FD of all baseball teams from 1871 to 2010. I used a select set of batting, fielding, and pitching statistics[ii], and you can see the data here. For the two teams that I pay the most attention to, I plotted their FD against wins, with World Series victories highlighted:

Given that these FD values represent how different the members of a team are, it's surprising that there is much of a pattern at all. But the negative relationship between wins and FD is strong and significant by several measures[iii]. So: the more similar a team is in terms of player statistics, the better the team does!

This pattern of less dissimilarity among players correlating with better performance at the team level has apparently been noticed before, by Stephen Jay Gould, who extrapolated this pattern also across teams to explain the gradual shrinking of differences among players over time:

"if general play has improved, with less variation among a group of consistently better payers, then disparity among teams should also decrease"

and so:

"As play improves and bell curves march towards right walls, variation must shrink at the right tail." (from "Full House", thanks to Marc for this quote!).

Interesting, but is it useful? One obvious drawback in this approach of examining variation in individual performance is that it ignores the fact that in baseball, we know that a high number of earned runs allowed is bad for a pitcher, and a low number for hits is bad for a hitter. In contrast, a high value for specific leaf area is neither good nor bad for a plant, just an indication of its nutrient acquisition strategy.

There are many exponentially more nerdy avenues to go with applying community ecology tools to baseball data, but I'll spare you from that for now!

What can community ecology learn from baseball?

One new baseball stat that gets a lot of attention during trades is 'wins above replacement'. This is such a complicated statistic to calculate that the "simple" definition is that for fielders, you add together wRAA and UZR, while for pitchers it is based off of FIP. I hope that cleared things up.

The point in the end is to say how many wins a player is worth, when compared to the average player. In ecology, the concept of 'wins above replacement' has at least two analogies.

First, community ecologists have been doing competition experiments since the dawn of time. The goal is to figure out what the effect of a species is at the community level, although fully factorial competition experiments at the community level are challenging to carry out. For example, Weigelt and colleagues showed that there can be non-additive effects of competitor plant species on a target species, but could rank the effect of competitors. This result allowed them to predict the effect of adding or removing a competitor species from a mixture, in a roughly similar way to how a general manager would want to know how a trade would change his or her team's performance.

Second, ecologists have shown that both niche complementarity and a 'sampling effect' are responsible for driving the positive relationship between biodiversity and ecosystem functioning. The sampling effect refers to the increasing chance of including a particularly influential species when the number of species increases. Large-scale experiments in grasslands have been carried out where plants are grown in monoculture and then many combinations, up to 60 species. The use of the monocultures allows an analysis similar in spirit to 'wins above replacement', by testing how much the presence of a particular species, versus the number of species, alters the community performance.

We could take this analogy further, and think of communities more like teams. A restoration ecologist might calculate 'wins above replacement' for all the species in a set of communities, and then create All Star communities from the top performers.

Lessons learned

A. Shockingly, there are baseball nerds, and there are ecology nerds, and there are even double-whammy basebology nerds.

B. There are quantitative approaches to analyzing individual performance in these crazily disparate realms which might be useful to each other.

C. I might need to spend more time writing papers and less time geeking out about baseball!

More analogies to consider:

Reciprocal transplants: trades?

Trophic levels: minor league system?

Nitrogen fertilization: steroids?

---

[i] One of the most astonishing databases around: complete downloadable stats for every player since 1871. This database is what NEON should aspire to be, except that this one was compiled completely privately by some single-minded and visionary baseball geeks!

[ii] Batting: Hits, at bats, runs batted in, stolen bases, walks, home runs

Fielding: Put outs, assists, errors, zone rating

Pitching: Earned run average, home runs allowed, walks, strike outs.

[iii] E.g. even after taking into account other more typical measures of success in offense (runs, R) and defense (runs allowed, RA), within years, there is still a negative slope for FD on wins:

lme(win ~ R + RA + FD, random = ~1|yearID, data = team)

Value Std.Err DF t-value p-value

(Intercept) 80.289 0.7411 2159 108.3 <0.001

R 0.107 0.0009 2159 116.8 <0.001

RA -0.105 0.0009 2159 -115.6 <0.001

FD -1.729 0.8083 2159 -2.1 0.0325

Predicting invader success requires integrating ecological and land use patterns.

Disclaimer, this was modified from an editorial I wrote for the Journal of Applied Ecology.

In the quest to understand species invasions, we often try to link the abundance and distribution of invaders to underlying ecological processes. For example, oft-studied are the links between exotic diversity and native richness or environmental heterogeneity. Seemingly independently, research into how specific land use or management activities affect invasion dynamics is also fairly common. While both research strategies are of fundamental importance, not often recognized, or at least explicitly studied, is that both ecological patterns and management activities simultaneously affect invasion success. Thus a truly integrative approach to understanding invader success must take into account variation in ecological communities and abiotic resource avalibility as well as land use patterns at multiple spatial scales. Such an approach is necessary if ecologists wish to predict potential invader abundance, spread and impact.

Diez et al. Examine how environmental and management heterogeneity interact to influence patterns of Hieracium pilosella (Asteraceae) inasions in the South Island of New Zealand. The spread of H. Pilosella in New Zealand is threatening native habitats (tussock fields) and the livestock grazing industry. Diez et al. Asked how environmental and management regimes affect H. Pilosella abundance and distribution across six large farms on the South Island. This is an interesting and important question, not just because they are examining how human-caused and ecological variation interact to affect H. Pilosella dynamics, but also because these sources are heterogeneity are realized at different spatial scales.

Diez et al. show that the abundance and distribution of H. Pilosella was significantly affected by the interaction of habitat type (i.e., short vs. tall tussocks) and farm management strategies (i.e., fertilization and grazing rates). At larger scales, H. Pilosella was more abundant in tall tussock habitats and was unaffected by fertilization, while in short tussocks, it was less abundant in fertilized patches. At small scales, H. Pilosella was less likely to be found in short tussocks with high exotic grass cover and high productivity (measured as site soil moisture and solar radiation). Conversely, in tall tussocks, H. Pilosella was more likely to be found on sites with high natural productivity. Diez et al. were able to tease these complex causal mechanism apart by using Bayesian multilevel linear models, for which they included example R code in an online appendix.

While it is a truism in ecology to say that heterogeneity affects ecological patterns, this paper deserves mention because they convincingly show that the spread of noxious exotic plants in a complex landscape, can potentially predicted by understanding the invader success in different habitat types and land management strategies. In their case they show how human activities, which were not designed to affect H. Pilosella, can strongly affect abundance in different habitat types. This type of approach to understanding invader dynamics can potentially arm managers with the ability to use existing land use strategies to predict how and where further invader targeting would be most useful.


Diez, J., Buckley, H., Case, B., Harsch, M., Sciligo, A., Wangen, S., & Duncan, R. (2009). Interacting effects of management and environmental variability at multiple scales on invasive species distributions Journal of Applied Ecology DOI: 10.1111/j.1365-2664.2009.01725.x

A roadmap to generalized linear mixed models

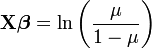In a recent paper in TREE, Ben Bolker (from the University of Florida) and colleagues describe the use of generalized linear mixed models for ecology and evolution. GLMMs are used more and more in evolution and ecology given how powerful they are, basically because they allow the use of random and fix effects and can analyze non-normal data better than other models. The authors made a really good job at explaining what to use when. Despite the fact that you need more than basic knowledge of stats to fully understand this guide, I think that people should take a look at it before starting to plan their projects, since it outlines really well all the possible alternatives (and challenges) that one can have when analyzing data. This article also describes what is available in each software package; this is really useful since is not obvious with program in SAS or R you need to use when dealing with some specific GLMMs.

Bolker, B., Brooks, M., Clark, C., Geange, S., Poulsen, J., Stevens, M., & White, J. (2009). Generalized linear mixed models: a practical guide for ecology and evolution Trends in Ecology & Evolution, 24 (3), 127-135 DOI: 10.1016/j.tree.2008.10.008

Shortening the R curve

I am a strong proponent of R for all data management, analysis and visualization. It is a truly egalitarian analysis package -open source and community-contributed analysis packages. The true power comes from complete control and automization of your analyzes as well as publicly accessible new functions created by members of the community. However, the drawback for a lot of people has been the rather steep learning curve, as with any programing language. But there are now a plethora of good books available that help shorten this curve. The Human Landscapes blog as reviewed and ranked introductory and reference R books, which should serve as an invaluable resource for those striving to become aRgonauts.